Authentication
Computer security authentication means verifying the identity of a user logging onto a network. Passwords, digital certificates, smart cards and biometrics can be used to prove the identity of the user to the network. Computer security authentication includes verifying message integrity, e-mail authentication and MAC (Message Authentication Code), checking the integrity of a transmitted message. There are human authentication, challenge-response authentication, password, digital signature, IP spoofing and biometrics.
Password
A password is a secret word or string of characters that is used for authentication, to prove identity or gain access to a resource (Example: An access code is a type of password). The password must be kept secret from those not allowed access. The use of passwords is known to be ancient. Sentries would challenge those wishing to enter an area or approaching it to supply a password or watchword. Sentries would only allow a person or group to pass if they knew the password. In modern times, user names and passwords are commonly used by people during a log in process that controls access to protected computer operating systems, mobile phones, cable TV decoders, automated teller machines (ATMs), etc. A typical computer user may require passwords for many purposes: logging in to computer accounts, retrieving e-mail from servers, accessing programs, databases, networks, web sites, and even reading the morning newspaper online.
To choose a good password
A good password is one that's hard to guess, yet easy to remember. So here are the top 10 ways to choose a password, in roughly increasing difficulty. If you don't use any of the first 5, you're well on your way. The stats are very rough estimates (for comparison purposes, an 8-character password is used for most calculations):
- Default (same as none):
- Many programs and services assign a default password . Change this to a new password immediately.
- examples: password, superuser
- 10 Common passwords:
- god, love, lust, money, private, qwerty, secret, sex, snoopy, & (surprise!) password
- Personal info:
- your name, initials, location (zip code), birthday, pets, license plate
- family/friend's names (including maiden), locations, birthdays, pets
- word/number combinations of any of the above
- Ego-related; examples: guru, master, wizard
- Favorite: Music (group names, albums), Fiction/Nonfiction/Comic books/characters, Movie/TV/Cartoon characters & titles
- Dumb Hollywood movie-people think all passwords are of this variety
- Categories:
- Double-words; examples: kittykitty, johnjohn
- Funny/nonsense/jargon words; examples: wassup, bzzzzz, foobar
- Insults; examples: biteme, eatdirt
- Keyboard sequences; examples: asdfg, qweasd, poiqwe
- Obscene words; examples: (use your imagination)
- Passwords based on host name (for people with lots of passwords)
- for example, if the system is named 'cat' an obvious password is catpass
- Reversals; examples: terces, wordpass, nhojnhoj
- Dictionary & Foreign Language words:
- If you can find your word here, it's not a very good password.
- Common Passwords - Various Languages
- Dan Klein - Browsable and categorized lists of English words
- DEC Collection - compressed lists of common English words
- stats: There's 200,000+ words in the English language (most people use around 10,000-40,000). As a guesstimate, there's some 32,000 8-letter words/phrases.
- For some word lists, see The Electronic Alveary
- Mixed-Case Dictionary Words (alternating UPPER-lower case letters)
- examples: paSSworD, PLaceBO
- stats: If a word has 2 letters, there's 4 (22) ways to capitalize it (at, At, aT, AT). If a word has 8 letters, there's 256 ways. Similar combinations (2letters) apply to each word in the dictionary. Guesstimate: There's around 32,000 8-letter words, which gives 8 million (32,000 x 256) mixed-case 8-letter passwords
- Mixed-case Word with Number(s)
- examples: 9fiNgeRS, loVELy68
- stats: Tacking on a number from 0-9 before or after a word gives 20 more variations to the password. Using 00-99 before or after the word, gives 200 variations. Guesstimate: there's some 19,000 6-letter words, and 243 million variations (19,000 x 64 x 200) of 6-letter-word 2-number passwords.
- Mixed-case Word(s)/Letter(s)
- Combining words and/or extra letters
- examples: GUessTHis, BiKeFisH
- stats: We're talking pretty big numbers here. Around 53 trillion (528) 8-letter mixed-case passwords (i.e. aaaaaaaa, aaaaaaaA, aaaaaaAa, ..., ZZZZZZZZ)
- Mixed-case Words/Numbers/Letters
- examples: No50WaY2, puT863MoX
- variant: Hacker/IRC/License-plate jargon
- examples: H4x0rD00dZ, UR2good4Me, FXR1stR8
- stats: OK, my mind's swimming, there's somewhere around 218 trillion (628) 8-letter/number passwords
- It takes an average of 5 seconds to crack this kind of password on a Windows machine; considerably longer on BSD or Linux.
- Random characters
- examples: qs3UIs82, k38#0J$dA
- note: some programs and services only allow letters and numbers, some include dashes ('-'); the best allow any character
- stats: Assuming 94 'type-able' characters, there's 6 gazillion (948 = 6.1 quadrillion [US]) different 8-character passwords. There's not as many 7-character passwords, but there's some 9-character ones still available, if you hurry.
In general:
- No password is uncrackable.
- The best you can do is make it difficult and non-trivial to determine your password.
- What's the worst password? The one you've forgotten.
- Whatever method you choose, it's a good idea to change your password often.
- The more important the password, the more often it should be changed.
- Why? If someone is attempting a brute-force attack on your password, the hope is that you're changing it to something they've already tried and found to be wrong.
- The longer the password, the harder it is to 'guess.'
- note: many systems limit passwords to 8 characters.
- Some clever people are foregoing brute-force hacks (e.g. dictionary attacks), in favor of 'social engineering' to obtain passwords.
- If somebody calls or emails, requesting your password, it's a dumb idea to give it to them.
- Of course nobody would sticky-note a password to their monitor, or under a keyboard
The concept of securing messages through cryptography has a long history. Indeed, Julius Caesar is credited with creating one of the earliest cryptographic systems to send military messages to his generals.
Throughout history, however, there has been one central problem limiting
widespread use of cryptography. That problem is key management. In
cryptographic systems, the term key refers to a numerical value used by an algorithm
to alter information, making that information secure and visible only to individuals
who have the corresponding key to recover the information. Consequently, the term
key management refers to the secure administration of keys to provide them to users
where and when they are required.
Historically, encryption systems used what is known as symmetric cryptography.
Symmetric cryptography uses the same key for both encryption and decryption.
Using symmetric cryptography, it is safe to send encrypted messages without fear of
interception (because an interceptor is unlikely to be able to decipher the message);
however, there always remains the difficult problem of how to securely transfer the
key to the recipients of a message so that they can decrypt the message.
A major advance in cryptography occurred with the invention of public-key
cryptography. The primary feature of public-key cryptography is that it removes the
need to use the same key for encryption and decryption. With public-key
cryptography, keys come in pairs of matched “public” and “private” keys. The
public portion of the key pair can be distributed in a public manner without
compromising the private portion, which must be kept secret by its owner. An
operation (for example, encryption) done with the public key can only be undone
with the corresponding private key.
Prior to the invention of public-key cryptography, it was essentially impossible to
provide key management for large-scale networks. With symmetric cryptography, as
the number of users increases on a network, the number of keys required to provide
secure communications among those users increases rapidly. For example, a network
of 100 users would require almost 5000 keys if it used only symmetric cryptography.
Doubling such a network to 200 users increases the number of keys to almost
20,000. Thus, when only using symmetric cryptography, key management quickly
becomes unwieldy even for relatively small-scale networks.
Encryption and digital signature
To better understand how cryptography is used to secure electronic communications,
let’s look at a process we are all familiar with: writing and sending a check.
Securing the electronic version
The simplest electronic version of the check can be a text file, created with a word
processor, asking your bank to pay someone a specific sum. However, sending this
check over an electronic network poses several security problems:
- • since anyone could intercept and read the file, you need confidentiality.
- • since someone else could create a similar counterfeit file, the bank needs to
authenticate that it was actually you who created the file.
- • since you could deny creating the file, the bank needs non-repudiation.
- • since someone could alter the file, both you and the bank need data
integrity.
To overcome these issues, Entrust performs a number of steps hidden behind a
simple user interface. The first step is to “sign” the check with a digital signature.
The process of digitally signing starts by taking a mathematical summary (called a hash code) of the check. This hash code is a uniquely-identifying digital fingerprint of the check. If even a single bit of the check changes, the hash code will dramatically change. The next step in creating a digital signature is to sign the hash code with your private key. This signed hash code is then appended to the check. How is this a signature? Well, the recipient of your check can verify the hash code sent by you, using your public key. At the same time, a new hash code can be created from the received check and compared with the original signed hash code. If the hash codes match, then the recipient has verified that the check has not been altered. The recipient also knows that only you could have sent the check because only you have the private key that signed the original hash code.
Confidentiality and encryption
Once the electronic check is digitally signed, it can be encrypted using a high-speed mathematical transformation with a key that will be used later to decrypt the document. This is often referred to as a symmetric key system because the same key is used at both ends of the process.
As the check is sent over the network, it is unreadable without the key. The next challenge is to securely deliver the symmetric key to the bank. Public-key cryptography for delivering symmetric keys Public-key encryption is used to solve the problem of delivering the symmetric encryption key to the bank in a secure manner. To do so, you would encrypt the symmetric key using the bank’s public key. Since only the bank has the corresponding private key, only the bank will be able to recover the symmetric key and decrypt the check.
Public Key InfrastructureThe Public Key Infrastructure (PKI) is a set of hardware, software, people, policies, and procedures needed to create, manage, store, distribute, and revoke digital certificates.
In cryptography, a PKI is an arrangement that binds public keys with respective user identities by means of a certificate authority (CA). The user identity must be unique for each CA. The binding is established through the registration and issuance process, which, depending on the level of assurance the binding has, may be carried out by software at a CA, or under human supervision. The PKI role that assures this binding is called the Registration Authority (RA) . For each user, the user identity, the public key, their binding, validity conditions and other attributes are made unforgettable in public key certificates issued by the CA. The term trusted third party (TTP) may also be used for certificate authority (CA).
The term PKI is sometimes erroneously used to denote public key algorithms, which do not require the use of a CA.
RSA
The RSA algorithm involves three steps: key generation, encryption and decryption.
RSA involves a public key and a private key. The public key can be known to everyone and is used for encrypting messages. Messages encrypted with the public key can only be decrypted using the private key. The keys for the RSA algorithm are generated the following way:
- Choose two distinct prime numbers p and q.
- Compute n = pq.
- n is used as the modulus for both the public and private keys
- Compute the totient:
 .
. - Choose an integer e such that
 , and e and
, and e and  share no divisors other than 1 (i.e. e and
share no divisors other than 1 (i.e. e and  are coprime).
are coprime). - Determine d (using modular arithmetic) which satisfies the congruence relation
 .
. - Stated differently, ed − 1 can be evenly divided by the totient (p − 1)(q − 1).
- This is often computed using the Extended Euclidean Algorithm.
- d is kept as the private key exponent.
The public key consists of the modulus n and the public (or encryption) exponent e. The private key consists of the modulus n and the private (or decryption) exponent d which must be kept secret.
Notes on some variants:
- For efficiency the following values may be precomputed and stored as part of the private key:
- p and q: the primes from the key generation,
 and
and  ,
,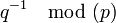 .
.
Alice transmits her public key (n,e) to Bob and keeps the private key secret. Bob then wishes to send message M to Alice.
He first turns M into an integer 0 < m < n by using an agreed-upon reversible protocol known as a padding scheme. He then computes the ciphertext c corresponding to:
This can be done quickly using the method of exponentiation by squaring. Bob then transmits c to Alice.
Alice can recover m from c by using her private key exponent d by the following computation:
Given m, she can recover the original message M by reversing the padding scheme.
The above decryption procedure works because:
 .
.
Now, since 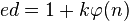 ,
,
 .
.
The last congruence directly follows from Euler's theorem when m is relatively prime to n. By using the Chinese remainder theorem it can be shown that the equations hold for all m.
This shows that we get the original message back:
A working example
Here is an example of RSA encryption and decryption. The parameters used here are artificially small, but one can also use OpenSSL to generate and examine a real keypair.
- Choose two prime numbers
- p = 61 and q = 53
- Compute n = pq
- Compute the totient

- Choose e > 1 coprime to 3120
- e = 17
- Compute d such that
 e.g., by computing the modular multiplicative inverse of e modulo
e.g., by computing the modular multiplicative inverse of e modulo  :
: - d = 2753
- since 17 · 2753 = 46801 and mod (46801,3120) = 1 this is the correct answer.
The public key is (n = 3233, e = 17). For a padded message m the encryption function is:
The private key is (n = 3233, d = 2753). The decryption function is:
For example, to encrypt m = 123, we calculate
To decrypt c = 855, we calculate
 .
.



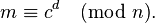





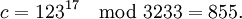













0 comments:
Post a Comment